Discussions with Teachers
GA 295
Discussion Four
25 August 1919, Stuttgart
Translated by Helen Fox
RUDOLF STEINER: We will now continue the work we have set out to do, and we will pass on to what will be said about how to deal with arithmetic from the perspective of the temperaments. We must primarily consider what procedure we should follow in teaching arithmetic.
Someone showed how to explain a fraction by breaking a piece of chalk.
RUDOLF STEINER: First, I have just one thing to say: I would not use chalk, because it is a great pity to break chalk. I would choose something less valuable. A bit of wood or something like that would do, wouldn’t it? It is not good to accustom young children to destroy useful things.
Question: Does a child who slouches and lacks a proper vertical position find it more difficult to understand spatial and geometrical forms because of such a problem?
RUDOLF STEINER: Not to any perceptible degree. Things of this kind depend more on the tendencies found in the construction of the human organism rather than on the build of an individual. This was once brought very forcibly to my attention after a lecture in Munich. I had explained in the lecture that it has a certain significance for the whole structure of the human being that the backbone is in line with the diameter of the Earth, while the line of the animal’s back is at a right angle to it. Afterward a learned doctor from Karlsruhe came and asserted that when a person is asleep the spine is in a horizontal position! I replied, “It’s not a question of whether a person can move the backbone into various positions, but that the whole human structure is arranged architecturally so that the backbone is ordinarily vertical, although it can be placed at a slant or any other position.”
If you did not consider this you could never understand how certain potentials found in the intellect appear, even when the senses themselves are not active—for example, in someone born blind. The human being is constructed so that the intellect has certain tendencies in the direction of the eyes, and thus, even in the case of those born blind, it is still possible to evoke mental images that are connected with the eyes, such as in the case of someone like the blind Helen Keller. What is important is the tendency, the general dispositions of the human organism, rather than what may be the result of a chance situation here or there. I would now like to add the following to what was said. It is not so much a question of criticizing these things, because that can always be done. What matters is that things of this kind are brought up and that we try to understand them.
Let’s start with addition, and first see what our view of addition should be. Let’s suppose I have some beans or a heap of elderberries. For our present task I will assume that the children can count, which indeed they must learn to do first. A child counts them and finds there are 27. “Yes,” I say. “27—that is the sum.” We proceed from the sum, not from the addenda. You can follow the psychological significance of this in my theory of knowledge.1See Rudolf Steiner, Goethe’s World View, and The Science of Knowing: Outline of an Epistemology Implicit in the Goethean World View, both Mercury Press, Spring Valley, NY, 1992 and 1988. We must now divide the whole into the addenda, into parts or into little heaps. We will have one heap of, let’s say, 12 elderberries, another heap of 7, still another of say 3, and one more, let’s say 5; this will represent the whole number of our elderberries: 27 = 12 + 7 + 3 + 5.
We work out our arithmetical process from the sum total 27. I would allow this process to be done by several children with a pronounced phlegmatic temperament. You will gradually come to realize that this kind of addition is particularly suited to the phlegmatics. Then, since the process can be reversed, I would call on some choleric children, and gather the elderberries together again, this time arranging them so that 5 + 3 + 7 + 12 = 27. In this way the choleric children do the reverse process. But addition in itself is the arithmetical rule particularly suited to phlegmatic children.
Now I choose one of the melancholic children and say, “Here is a little pile of elderberries. Count them for me.” The child discovers that there are, let’s say, 8. Now, I say, “I don’t want 8, I only want 3. How many elderberries must you take away to leave me only 3?” The child will discover that 5 must be removed. Subtraction in this form is the one of the four rules especially suited to melancholic children.
Then I call on a sanguine child to do the reverse process. I ask what has been taken away, and I have this child tell me that if I take 5 from 8, I’ll have 3 left. Thus, the sanguine child does the reverse arithmetical process. I would only like to add that the melancholic children generally have a special connection with subtraction when done as I have described.
Now I take a child from the sanguine group. Again I put down a pile of elderberries, but I must be sure the numbers fit. I must arrange it beforehand, otherwise we find ourselves involved in fractions. I have the child count out 56 elderberries. “Now look; here I have 8 elderberries, so now tell me how many times you find 8 elderberries contained in 56.” So you see that multiplication leads to a dividing up. The child finds that the answer is 7. Now I let the sum be done in reverse by a melancholic child and say, “This time I do not want to know how often 8 is contained in 56, but what number is contained 7 times in 56." I always allow the reverse process to be done by the opposite temperament.
Next I introduce the choleric to division, from the smaller number to the greater, by saying, “Look, here you have a little pile of 8; I want you to tell me what number contains 8 seven times.” Now the child must find the answer: 56, in a pile of 56. Then I have the phlegmatic children work out the opposite process: ordinary division. The former is the way I use division for the choleric child, because the rule of arithmetic for the choleric children is mainly in this form division.
By continuing in this way I find it possible to use the four rules of arithmetic to arouse interest among the four temperaments. Adding is related to the phlegmatic temperament, subtracting to the melancholic, multiplying to the sanguine, and dividing—working back to the dividend—to the choleric. I ask you to consider this, following what N. has been telling us.
It is very important not to continue working in a singular way, doing nothing but addition for six months, then subtraction, and so on; but whenever possible, take all four arithmetical rules fairly quickly, one after another, and then practice them all—but at first only up to around the number 40. So we shall not teach arithmetic as it is done in an ordinary curriculum. By practicing these four rules, however, they can be assimilated almost simultaneously. You will find that this saves a great deal of time, and in this way the children can work one rule in with another. Division is connected with subtraction, and multiplication is really only a repetition of addition, so you can even change things around and give subtraction, for example, to the choleric child.
It was suggested that one begin with solid geometry.
RUDOLF STEINER: With adults it is possible to begin with solids, but why should you want to go from solids to plane surfaces with a child? You see, three-dimensional space is never easy to picture, least of all for a child. You cannot impart anything to a child but a vague idea of space. Indeed, the child’s imagination will suffer if expected to imagine solid bodies.
You are assuming that the solid is the actual thing and the line abstract; but this is not so. A triangle is in itself something very concrete; it exists in space. Children see things mainly in surfaces. It is an act of violence to force a child into the third dimension, the idea of depth. If children are to apply their imagination to a solid, then they must first have the necessary elements within to build up this imaginative picture. For example, children must really have a clear picture of a line and a triangle before a tetrahedron can be understood. It is better for them to first have a real mental picture of a triangle; the triangle is an actuality, not merely an abstraction taken from the solid.
I would recommend that you teach geometry, not as solid geometry first, but as plane geometry, giving figures with plane surfaces between them; this is preferable, because children like to use their powers of understanding for such things; beginning with plane geometry will support them. You can add further to the effect by connecting it with drawing lessons. Children can draw a triangle relatively early, and you should not wait too long before having them copy what they see.
The figure shown yesterday was repeated, this time for a choleric child and for a phlegmatic child.
RUDOLF STEINER: That is a very good design for the choleric child. For the phlegmatic child I would prefer to make it speckled, I would rather have it checkered. It would be possible to use your design, but it would not arouse the phlegmatic child’s attention enough.
The drawings for the melancholic and the sanguine child were presented.
RUDOLF STEINER: In using this method you will find that the needs of the sanguine and melancholic child can be met in the following ways. For the sanguine you should constantly make use of varied repetition. You might have the child draw a design like this:

And then three more like it:
and then one more, so that the emphasis is on repetition:

For the melancholic child it would be good to give a design in which careful thought plays some part.
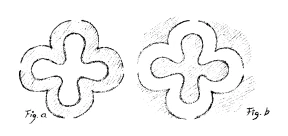
Suppose you have a melancholic child first draw a form like this (figure a), and then the counter-form (figure b), so that they complement one another. This will arouse the child’s imagination. I will shade the original form like this (a) and the opposite form like this (b) and you will see that what is shaded in one form would be left blank in the other. If you think of the blank part as filled in, you would get the first form again. In this way the outer forms in the second drawing are the opposite of the inner, and this design is the opposite of those based on repetition. Choose something requiring thought and connected with observation for the melancholic children, and something in which repetition plays a part (creepers, tendrils, and so on) for the sanguine children.
The story of “Mary’s Child” was told in the style for phlegmatic children.
RUDOLF STEINER: It is important to cultivate well-articulated speech and then help the children to get out of their dialect.2This does not imply that Rudolf Steiner was unaware of the importance of dialect in its right place. Frau Dr. Steiner will demonstrate.
Someone told the story of “The Long-Tailed Monkey” for phlegmatic children.
RUDOLF STEINER: For a story of this kind there are certain aids to storytelling that I would suggest you use. Just for the phlegmatics it would be good to pause occasionally mid-sentence, look at the children, and use the pause to let the imagination work. You can arouse their curiosity at critical points so that they can think on in advance a little and complete the picture for themselves. “The king’s daughter ... was ... very beautiful ... but ... she was not equally ... good.” This use of pauses in narration works strongest with phlegmatic children.
A fairy story was told for phlegmatic children.
RUDOLF STEINER: You must make use of a moment of surprise and curiosity.
Someone told an animal story for sanguine children about a horse, a donkey, and a camel. “Which do you like best, the horse or the donkey?”
RUDOLF STEINER: Some melancholics will prefer the donkey. With these descriptions of animals I would ask you to remember that, as far as possible, they should lead the child to observe animals, for descriptions of this kind can contain true natural history.
Someone else told the story of a monkey who escaped into the rafters—first for sanguines and then for melancholics.
RUDOLF STEINER: Yes, in certain cases that would make a very good impression on the melancholic children, but here also it is my opinion that you could develop it a little further in order to encourage animal observation as such.
I would like to remind you that consideration of the child’s temperament should not be neglected, but you can safely use the first three to five weeks to observe the temperaments of your pupils and then divide them into groups as spoken of here.
It would also be good to consider the extremes of the various temperaments. Goethe’s world view led him to express the beautiful idea that one can understand the normal by studying the abnormal. Goethe views an abnormal plant—a misshapen plant—and from the nature of the malformation he learns to understand the normal plant. In the same way you can find the connections between the absolutely normal and the malformations of the body-soul nature, and you yourselves can find the way from the temperaments to what is abnormal in the soul life.
If the melancholic temperament becomes abnormal and does not remain within the boundaries of the soul, but rather encroaches on the body, then insanity arises. Insanity is the abnormal development of a predominantly melancholic temperament. The abnormal development of the phlegmatic temperament is mental deficiency. The abnormal development of the sanguine is foolishness, or stupidity. The abnormal development of the choleric is rage. When a person is in an emotional state you will sometimes see these attacks of insanity, mental deficiency, foolishness, or rage arising from otherwise normal soul conditions. It is indeed necessary that you focus your attention and observation on the entire soul life.
Now we will move on to the solution of our other problem. I said: Suppose that you, my friends, had children of eight or nine years old in your class. What would you do if, three or four weeks after the beginning of term, you noticed that a phlegmatic, a choleric, and a melancholic child were, to some extent, becoming the three “Cinderellas” of the class, so that all the others pushed them around and no one wanted to play with them and so on? If this had happened, what would you as teachers do about it?
Various teachers expressed opinions.
RUDOLF STEINER: You should never allow the children to inform against each other; you must find other ways of discovering what has caused them to be “Cinderellas.” As teachers, you see, you will often find that you have to help raise the children. If they get into all sorts of naughty ways, their fathers and mothers will come and say, for example, “My child tells lies.” You would seldom go wrong to give this advice: say to the parents, “Imagine a case, a story, in which an untruthful child is placed in a ridiculous position—where the child, because of lying, is led into a situation that appears absurd even to the child. If you tell the child a story of this kind, and then another, and still another like it, you will as a rule cure your child of the tendency to lie.”
Similarly, you will find it helpful to insert into a story everything that has been said about the three “Cinderellas,” everything you can hear and discover about these children, and then you can tell this story to the whole class. The effect of this will be that the three “Cinderellas” will be somewhat comforted and the others somewhat ashamed. If you do this you will certainly find that, even at the first attempt, and even more after the second, you will succeed in restoring a friendly, social atmosphere, a mutual sympathy among the children. You should continue with a similar story throughout the term.
Tomorrow we will take another case that also happens sometimes, which certainly cannot be treated by telling a story that comforts some of the children and shames the others. Suppose you had children of eight or nine years old in your class, and one of these small fries had discovered a particularly mischievous trick. These things do happen. It had been learned outside the school and succeeded in infecting all the others so that the whole class was at it during recess.
An ordinary schoolmaster would go to the extreme of punishing the whole class, but I hope that by tomorrow you will think of a more rational—that is a more effective—method, because this old way of punishing places the teacher in the wrong relationship with the children, and this will not fail to have an effect. The aftereffect is not good.
I have a special case in mind that really happened, where a certain teacher did not act very wisely. One little rascal had conceived the idea of spitting on the ceiling and had actually succeeded. It was a long time before the teacher discovered the culprit. He could not pick out any one child, because they had all done it; the whole classroom was damaged.
Please think over this case of moral delinquency by tomorrow. All you really know is that the whole class had been infected. You cannot begin with the assumption that you know who the ringleader was. You will have to consider whether it wouldn’t be better to give up all thought of discovering the culprit by getting the children to tell on each other. How would you act in this case?

