Discussions with Teachers
GA 295
Second Lecture on the Curriculum
6 September 1919 A.M., Stuttgart
Translated by Katherine E. Creeger
Now it’s time to divide up the rest of the subjects and distribute them among the various grades.
It should be very clear that when the children are going on nine—that is, in the third grade—they should begin to study an appropriate selection of animals, which we must always relate to the human being, as in the example I presented to you.1See Practical Advice to Teachers, Rudolf Steiner Press, London, 1988, lecture 7. This should be continued in the fourth grade, so that during the third and fourth grades we consider the animal kingdom scientifically in its relationship to the human being.
In the fifth grade, we begin to add less familiar animals. We also begin the study of botany as I described it in the theoretical portion of our seminar.2See discussion 9, page 114. In the sixth grade, we continue with botany and begin the study of minerals, which should definitely be done in conjunction with geography.
In the seventh grade we return to the human being and attempt to teach what I pointed to yesterday with regard to what people need to learn about health and nutrition. We also attempt to apply the concepts the children have acquired in the fields of physics and chemistry to developing a comprehensive view of some specific commercial or industrial processes. All this should be developed out of science, in connection with what we are teaching in physics, chemistry, and geography.
In the eighth grade you will have to construct the human being by showing what is built in from the outside—the mechanics of the bones and muscles, the inner structure of the eye, and so on. Once again, you present a comprehensive picture of industrial and commercial relationships as they relate to physics, chemistry, and geography. If you build up your science lessons as we have just described, you will be able to make them incredibly lively and use them to awaken the children’s interest in everything present in the world and in the human being.
Instruction in physics begins in the sixth grade and is linked to what the children have learned in music. We begin the study of physics by allowing acoustics to be born out of music. You should link acoustics to music theory and then go on to discuss the physiology of the human larynx from the viewpoint of physics. You cannot discuss the human eye yet, but you can discuss the larynx. Then, taking up only the most salient aspects, you go on to optics and thermodynamics. You should also introduce the basic concepts of electricity and magnetism now.
The following year, in the seventh grade, you expand on your studies of acoustics, thermodynamics, optics, electricity, and magnetism. Only then do you proceed to cover the most important basic concepts of mechanics—the lever, rollers, wheel and axle, pulleys, block and tackle, the inclined plane, the screw, and so on. After that you start from an everyday process such as combustion and try to make the transition to simple concepts of chemistry.
In the eighth grade you review and expand upon what was done in the seventh and then proceed to the study of hydraulics, of the forces that work through water. You cover everything belonging to hydraulics—water pressure, buoyancy, Archimedes’ principle.
It would be great if we could stay here for three years giving lectures on education and providing examples of all the things you will have to figure out how to do yourselves out of your own inventiveness, but that can’t be. We will have to be content with what has already been presented.
You conclude your study of physics, so to speak, with aerodynamics—that is, the mechanics of gases—discussing everything related to climatology, weather, and barometric pressure. You continue to develop simple concepts of chemistry so that the children also learn to grasp how industrial processes are related to chemical ones. In connection with chemical concepts, you also attempt to develop what needs to be said about the substances that build up organic bodies—starch, sugar, protein, and fat.
We must still apportion everything related to arithmetic, mathematics, and geometry and distribute it among the eight grades.
You know that standard superficial methodology dictates that in the first grade we should deal primarily with numbers up to 100. We can also go along with this, because the range of numbers doesn’t really matter in the first grade, where we stick with simpler numbers. The main issue, regardless of what range of numbers you use, is to teach the arithmetical operations in a way that does justice to what I said before: Develop addition out of the sum, subtraction out of the remainder, multiplication out of the product and division out of the quotient—that is, exactly the opposite of how it’s usually done. Only after you have demonstrated that 5 is 3 plus 2, do you demonstrate the reverse—that adding 2 and 3 yields 5. You must arouse in the children the powerful idea that 5 equals 3 plus 2, but that it also equals 4 plus 1, and so on. Thus, addition is the second step after separating the sum into parts, and subtraction is the second step after asking “What must I take away from a minuend to leave a specific difference?” and so on. As I said before, it goes without saying that you do this with simpler numbers in the first grade, but whether you chose a range of up to 95 or 100 or 105 is basically beside the point.
After that, however, when the second dentition is over, we can immediately begin to teach the children the times tables—even addition, as far as I’m concerned. The point is that children should memorize their times tables and addition facts as soon as possible after you have explained to them in principle what these actually mean—after you have explained this in principle using simple multiplication that you approach in the way we have discussed. That is, as soon as you’ve managed to teach the children the concept of multiplication, you can also expect them to learn the times tables by heart.
Then in the second grade you continue with the arithmetical operations using a greater range of numbers. You try to get the students to solve simple problems orally, in their heads, without any writing. You attempt to introduce unknown numbers by using concrete objects—I told you how you could approach unknown numbers using beans or whatever else is available. However, you should also not lose sight of doing arithmetic with known quantities.
In the third grade everything is continued with more complicated numbers, and the four arithmetical operations practiced during the second grade are applied to certain simple things in everyday life.
In the fourth grade we continue with what was done in the earlier grades, but we must now also make the transition to fractions and especially to decimal fractions.
In the fifth grade, we continue with fractions and decimals and present everything the children need to do independent calculations involving whole numbers, fractions, and decimals.
In the sixth grade we move on to calculating percentages, interest, discounts and the interest on promissory notes, which then forms the basis for algebra, as we have already seen.
I ask you to observe that, until the sixth grade, we have been deriving the geometric shapes—circle, triangle, and so on—from drawing, after having done drawing for the sake of writing in the first few years. Then we gradually made the transition from drawing done for the sake of writing to developing more complicated forms for their own sake—that is, for the sake of drawing, and also to do painting for the sake of painting. We guide instruction in drawing and painting into this area in the fourth grade, and in drawing we teach what a circle is, what an ellipse is, and so on. We develop this out of drawing. We continue this by moving on to three-dimensional forms, using plasticine if it’s available, and whatever else you can get if it isn’t—even if it’s mud from the street, it doesn’t matter! The point is to develop the ability to see and sense forms.
Mathematics instruction, geometry instruction, then picks up on what has been taught in this way in the drawing classes. Only then do we begin to explain in geometrical terms what a triangle, a square, or a circle is, and so on. That is, the children’s spatial grasp of form develops through drawing. We begin to apply geometrical concepts to what they have learned in this way only once they are in the sixth grade. Then we have to make sure that we do something different in drawing.
In the seventh grade, after making the transition to algebra, we teach raising numbers to powers and extracting roots, and also what is known as calculating with positive and negative numbers. Above all, we try to introduce the children to what we might call practical, real-life applications of solving equations.
We continue this in the eighth grade and take the children as far as they can get with it. We also add calculating areas and volumes and the theory of geometrical loci, which we at least touched upon yesterday.
This gives you a picture of what you have to do with the children in mathematics and geometry.

As we have already seen, in the drawing lessons in the first few grades, we first teach the children to have a specific feeling for rounded or angular forms, and so on. From these forms, we develop what we need for teaching writing. In these very elementary stages of teaching drawing, we avoid imitating anything. As much as possible, you should initially avoid allowing the children to copy a chair or a flower or anything else. As much as possible, you should have them produce linear forms—forms that are round, pointed, semicircular, elliptical, straight, and so on. Awaken in the children a feeling for the difference between the curve of a circle and the curve of an ellipse. In short, awaken their feeling for form before their urge to imitate wakes up! Wait until later before allowing them to apply what they have practiced in drawing forms to imitating actual objects. First have them draw angles so that they understand what an angle is through its shape. Then you show them a chair and say, “Look, here’s an angle, and here’s another angle,” and so on. Do not let the children imitate anything until you have cultivated their feeling for independent forms which can be imitated later. Stick to this principle even when you move on to a more independent and creative treatment of drawing and painting.
Then in the sixth grade you introduce simple projection exercises and drawing shadows, both freehand and with a ruler and compass and the like. Make sure that the children have a good grasp of the concept and can reproduce in their drawings what the shadow of a sphere looks like on the surface of a cylinder if the cylinder is here and the sphere here and a light is shining on the sphere:
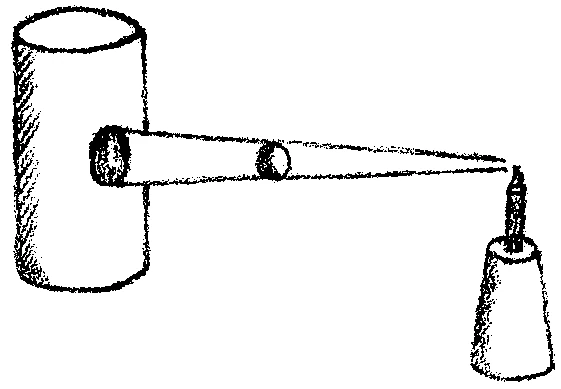
Yes, how shadows are cast! So a simple study of projection and shadows must take place in the sixth grade. The children must get a conception of it and must be able to imitate how more or less regular shapes or physical objects cast their shadows on flat and curved surfaces. In their sixth school year the children must acquire a concept of how the technical aspect unites with the element of beauty, of how a chair can be technically suited for a certain purpose while also having a beautiful form. The children must acquire both a concept and a handson grasp of this union of the technical and the beautiful.
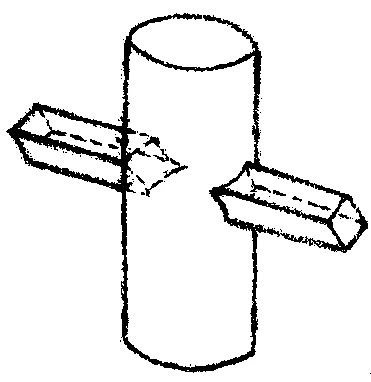
Then, in the seventh grade, everything having to do with one object penetrating another should be covered. As a simple example, you might say, “Here we have a cylinder with a post running through it. The post has to go through the cylinder.” You must demonstrate what kind of a shape the post cuts in the surface of the cylinder when it enters and exits. This is something to learn together with the children. They must learn what happens when objects or surfaces interpenetrate, so that they know that it makes a difference whether a stovepipe goes through the ceiling at a right angle, in which case their intersection is a circle, or at an angle, in which case it is an ellipse. In addition, this is the year when the children must be taught a good conception of perspective. So you do simple perspective drawing with objects foreshortened in the distance and elongated in the foreground, and you draw objects that are partially concealed and so on. Once again, you combine the technical aspect with beauty, so that you awaken in the children an idea of whether or not it is beautiful when some portion of a wall of a house is concealed by a projection, let’s say. Some such projections are beautiful and others are not. These things have a pronounced effect when they are taught to seventh graders in particular—that is, to thirteen- or fourteen-year-olds.
In the eighth grade, all this is raised to an artistic level. All the other subjects must be handled similarly to the ones we have discussed. We will come back to this in the afternoon and still add a few things to complete our curriculum. Above all, we will have to see how music is developed in the first grade out of elements that are as simple and elementary as possible, and how from the third grade on the transition is made to more complicated things. The point is that the children should be able to take in those aspects of playing an instrument—especially of playing an instrument, but also of singing—that have a creative and formative effect on their capabilities.
As special cases among all the other artistic subjects, we will have to emphasize gymnastics and eurythmy, which must both be developed out of the element of music and the other arts.

