The Fourth Dimension
GA 324a
Second Lecture
31 March 1905, Berlin
Today I will discuss elementary aspects of the idea of multidimensional space, with particular reference to the thoughts of Charles Hinton, a very wise man. [Note 18] As you recall, last time we began by considering the zero dimension and moved on to multidimensional space. Let me briefly reiterate the ideas we developed about two- and three-dimensional space.
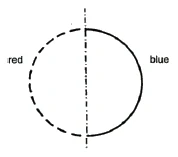
What do we mean by a symmetrical relationship? How do I make two plane figures that are mirror images of each other, such as this red figure and this blue one, coincide? This is relatively easy to do with two half circles. I simply insert the red one into the blue one by rotating it (Figure 10). This is not so easy with the mirror-image symmetry below (Figure 11). No matter how I try to insert the red part into the blue part, I cannot make them coincide if I remain within the plane. There is a way to accomplish this, however, if we leave the board—that is, the second dimension—and use the third dimension,—in other words, if we lay the blue figure on top of the red by rotating it through space around the axis of reflection.

The situation is similar with a pair of gloves. We cannot make the one coincide with the other without leaving three-dimensional space. We have to go through the fourth dimension.
Last time I said that if we want to acquire an idea of the fourth dimension, we must allow relationships in space to remain fluid in order to produce circumstances similar to those present when we make the transition from the second to the third dimension. We created interlocking spatial figures from strips of paper and saw that interlocking brings about certain complications. This is not just a game, because such interlocking occurs everywhere in nature, especially in the intertwined motions of material objects. These motions include forces, so the forces also are intertwined. Take the Earth's movement around the Sun in connection with the Moon's movement around the Earth. The Moon describes a circle that winds around the Earth's orbit around the Sun,—that is, the Moon describes a spiral around a circle. Because of the Sun's own movement, however, the Moon makes an additional spiral around it, resulting in very complicated lines of force that extend throughout space.
The relationships of the heavenly bodies resemble Simony's twisted strips of paper, which we looked at last time. We must realize, as I said earlier, that we are dealing with complicated spatial concepts that we can understand only if we do not allow them to become fixed. If we want to understand the nature of space, we will have to conceive of it as immobile, initially, but then allow it to become fluid again. It is like going all the way to zero, where we find the living essence of a point.
Let's visualize again how the dimensions are built up. A point is zero dimensional, a line is one dimensional, a surface two dimensional, and a solid object is three dimensional. Thus, a cube has three dimensions: height, width, and depth. How do spatial figures of different dimensions relate to one another? Imagine being a straight line. You have only one dimension and can move only along a line. If such one-dimensional beings existed, what would their idea of space be? They would not be able to perceive their one-dimensionality. Wherever they went, they would be able to imagine only points, because points are all we can draw while remaining within a straight line. A two-dimensional being would encounter only lines,—that is, it would perceive only one-dimensional beings. A three-dimensional being, such as a cube, would perceive two-dimensional beings but not its own three dimensions.
Human beings, however, can perceive their own three dimensions. If we draw the correct conclusion, we must realize that if a one-dimensional being can perceive only points, a two-dimensional being only straight lines, and a three-dimensional being only surfaces, a being who perceives three dimensions must be four dimensional. The fact that we can delineate external beings in three dimensions and manipulate three-dimensional spaces means that we ourselves must be four-dimensional. Just as a cube would be able to perceive only two dimensions and not its own third dimension, it is clear that we cannot perceive the fourth dimension in which we ourselves live. Thus you see that human beings must be four-dimensional beings. We float in the sea of the fourth dimension like ice in water.
Let's return to our discussion of mirror images (Figure 11). This vertical line represents a cross-section formed by a mirror. The mirror reflects an image of the figure on the left side. The reflection process points beyond the second dimension into the third. In order to understand the direct, uninterrupted relationship of the mirror image to the original, we must assume that a third dimension exists in addition to the first and second.

Now let's consider the relationship between external space and internal perception. A cube outside me appears as a perception inside me (Figure 12). My idea of the cube relates to the cube itself as a mirror image relates to the original. Our sensory apparatus develops a mental image of the cube. If we want to make this image coincide with the original cube, we must pass through the fourth dimension. Just as a two-dimensional mirroring process must pass through the third dimension, our sensory apparatus must be four-dimensional to be able to bring about a direct connection between a mental image and an outer object. [Note 19] If you were to visualize in two dimensions only, you would confront merely a dream image. You would have no idea that an actual object exists in the outer world. When we visualize an object, we spread our capacity for mental pictures directly over outer objects by means of four-dimensional space.
In the astral state during earlier periods of human evolution, human beings were only dreamers. The only images arising in their consciousness were dream images. [Note 20] Later, humans made the transition from the astral state to physical space. Having said this, we have defined the transition from astral to physical, material existence in mathematical terms: before this transition, astral humans were three-dimensional beings,—therefore, they could not extend their two-dimensional mental images to the objective, three-dimensional, physical, material world. When human beings themselves became physical, material beings, they acquired the fourth dimension and therefore also could experience life in three dimensions.
The unique structure of our sensory apparatus enables us to make our mental images coincide with outer objects. By relating our mental images to outer things, we pass through four-dimensional space, putting the mental image over the outer object. How would things look from the other side, if we could get inside them and see them from there? To do so, we would have to go through the fourth dimension. The astral world itself is not a world of four dimensions. Taken together with its reflection in the physical world, however, it is four-dimensional. When we are able to survey the astral and physical worlds simultaneously, we exist in four-dimensional space. The relationship of our physical world to the astral world is four-dimensional.
We must learn to understand the difference between a point and a sphere. In reality, a point such as the one pictured here is not passive, but radiates light in all directions (Figure 13).
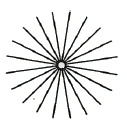
What would the opposite of such a point be? Just as the opposite of a line running from left to right is a line running from right to left, a point radiating light also has an opposite. Imagine a gigantic sphere, an infinitely large sphere that radiates darkness inward from all sides (Figure 14). This sphere is the opposite of a point that radiates light.

The true opposite of a light-radiating point is an infinite space that is not passively dark but actively floods space with darkness from all directions. The source of darkness and the source of light are opposites. We know that a straight line that vanishes into infinity returns to the same point from the other side. Similarly, when a point radiates light in all directions, the light returns from infinity as its opposite, as darkness.
Now let's consider the opposite case. Take the point as a source of darkness. Its opposite is then a space that radiates light inward from all directions. As I explained in the previous lecture, a point moving on a line does not vanish into infinity,—it returns from the other side (Figure 15).
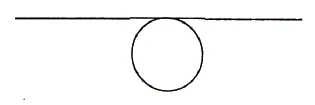
Analogously, a point that expands or radiates does not vanish into infinity,—it returns from infinity as a sphere. The sphere is the opposite of the point. Space dwells within the point. The point is the opposite of space.
What is the opposite of a cube? Nothing less than the totality of infinite space minus the part defined by the cube. We must imagine the total cube as infinite space plus its opposite. We cannot get by without polarities when we attempt to imagine the world in terms of dynamic forces. Only polarities give us access to the life inherent in objects.
When occultists visualize a red cube, the rest of space is green, because red is the complementary color of green. Occultists do not have simple, self-contained mental images. Their mental images are alive rather than abstract and dead. Our mental images are dead, while the objects in the world are alive. When we dwell in our abstract mental images, we do not dwell in the objects themselves. When we imagine a star that radiates light, we must also imagine its opposite—that is, infinite space—in the appropriate complementary color. When we do such exercises, we can train our thinking and gain confidence in imagining dimensions.
You know that a square is a two-dimensional area. A square composed of two red and two blue smaller squares (Figure 16) is a surface that radiates in different directions in different ways. The ability to radiate in different directions is a three-dimensional ability. Thus we have here the three dimensions of length, width, and radiant ability.

What we did here with a surface also can be done with a cube. Just as the square above is composed of four sub-squares, we imagine a cube composed of eight sub-cubes (Figure 17). Initially, the cube has three dimensions: height, width, and depth. In addition, we must distinguish a specific light-radiating capacity within each sub-cube. The result is another dimension, radiant ability, which must be added to height, width, and depth.

If every one of the eight sub-cubes has a different capacity to radiate, then, if I have just one cube with its one-sided capacity to radiate and I want to get a cube that radiates in all directions, I have to add another one in all directions, double it with its opposites—I have to compose it out of 16 cubes? [Note 21]
Next time we meet, we will learn ways of imagining higher-dimensional space.
Charles Howard Hinton (1853-1907), mathematician and author. Hinton was strongly influenced by his father, James Hinton (1822–1875), a surgeon who also wrote essays, including several on the art of thinking, or "thought-artistry,” in which he rejected any artificial restraints on thinking and experience due to religious, social, or legal regulation of behavior. Through his parents' contact with Mary Everest Boole (1832-1916), the widow of the logician and mathematician George Boole, (1815-1864) Hinton met the Booles' daughter, Mary Ellen, his future wife. Hinton studied mathematics at Oxford and taught at various institutions before leaving England for Japan in 1886. He lived in Japan until 1891 and then spent the rest of his life in the United States.
Hinton's search for certainty provoked a severe crisis in 1875. He resorted to the idea that only the arrangement of objects in space could lead to absolutely certain knowledge. In his preoccupation with thought exercises and visualizations concerning the arrangement of a cube subdivided into smaller cubes, he attempted to free himself from all subjectively imposed limitations such as the concepts of "above" and "below" ("Casting Out the Self" [1886], pp. 205-229). In this process, he encountered the problem of mirror-image subdivisions of two cubes and wondered whether this phenomenon might not also prove to be subjectively determined. While investigating this question, he discovered a treatise by Friedrich Zöllner on four-dimensional space [1878e] in the Quarterly Journal of Science (edited by William Crookes). In this paper, Zöllner briefly presented his experiments and views on the reality of the fourth dimension. Crookes (a chemist and physicist) and Zöllner both belonged to the group of university-based researchers who were attempting, though with little success, to use scientific methods to approach spiritualism.
Hinton spent the rest of his life studying the problem of the fourth dimension. His works concentrated on popularizing ideas about four-dimensional space and dealt especially with how to acquire the ability to visualize it. In this connection, Hinton studied the transition from the second to the third dimension in many different ways in order to create a solid foundation for depicting the fourth dimension in three-dimensional perceived space. In particular, he developed methodical exercises for acquiring a consistent view of three-dimensional space and for a time held the opinion that it was possible to acquire a non-sensory view of four-dimensional space in the same way (see A New Era of Thought [1900] and The Fourth Dimension [1904]). Hinton believed that the world included a material extension into the fourth dimension and attempted to prove this hypothesis through various experiments in psychology and physics. This view met with resistance both from materialists, who accepted the existence of only three spatial dimensions, and from spiritualists, who preferred to interpret the fourth dimension as purely spiritual in character (see Ballard [1980]). Hinton was a controversial writer who was avidly read and highly esteemed by the lay public, especially theosophists and avant-garde artists (see Henderson [1983] and [1988]). He was rejected or ignored in academic circles.
See the corresponding explanations in the previous lecture
See Rudolf Steiner, An Outline of Esoteric Science (GA 13), chapter IV: "Cosmic Evolution and the Human Being."
A definitive reconstruction of what Steiner meant by this analogy is not possible, and there is nothing in Hinton's works that corresponds to this train of thought. Although Hinton also uses colors to illustrate the transition from the second to the third dimension and especially the transition from the third to the fourth, he uses them very differently. In his lecture of May 24, 1905, reprinted in this volume, Steiner gives a review of Hinton's thoughts on this subject.
The geometric basis of the thoughts Steiner presents here is as follows: A line segment bisected in the middle can be developed into a square by allowing each half of the segment to form the shared side of two adjacent smaller squares. The result is a larger square divided into four smaller ones (Figure 16). A cube divided into eight smaller cubes can then be constructed by allowing each of the smaller squares to form the shared surface of two adjacent cubes (Figure 17). The corresponding four-dimensional figure, the four-dimensional cube, results when each of the eight sub-cubes of the three-dimensional cube is interpreted as the shared boundary between two four-dimensional cubes. The result is a four-dimensional cube divided into sixteen sub-cubes.

